Return to Course Home Page

Session 3-1: Introduction to NumPy

⬅️ Previous Session | 🏠 Course Home | 🚦 EDS217 Vibes | ➡️ Next Session |

Having covered the basics of Python, we will now explore its applications for data science. Bypassing the hype, data science is an interdisciplinary subject that lies at the intersection of statistics, computer programming, and domain expertise. It is best to think of data science not as a new field of knowledge itself, but rather as a set of skills for analysing and interrogating datasets within your existing area of expertise – in our case, environmental science and management.

datascience

Python’s extensive, active “ecosystem” of packages like NumPy, Pandas, SciPy, and Matplotlib – all of which we will explore in this next set of sessions – lends itself well to data analysis and scientific computing. In addition, this section outlines techniques for importing, manipulating, visualizing, and exporting data in Python.

While data come in a wide variety of formats, it is useful to conceptualize all data as arrays of numbers (recall the spreadsheet analogy from Session 1-4). For example, an image is, at its core, a two-dimensional array of numbers representing the brightness of each pixel across the image area. When envisioned this way, it is easy to see how the image can be transformed and analysed by manipulating values in the array:

imagearray

Session Topics
  • 📌 NumPy Arrays
    • Constructing arrays from lists
    • Constructing arrays from scratch
  • 📌 Array Manipulation
    • Array attributes
    • Indexing + slicing
    • Array reduction
    • Reshaping, resizing, + rearranging arrays
    • Joining + splitting arrays
  • 📌 Array Math
    • Universal functions
    • Array-to-array math: broadcasting
  • 📌 Handling missing data 
Readings
This notebook is designed to be run as a stand alone activity. However, the material covered can be supplemented by <a href="https://proquest-safaribooksonline-com.proxy.library.ucsb.edu:9443/book/programming/python/9781491912126/2dot-introduction-to-numpy/introduction_to_numpy_html"> Chapter 2</a> of the <a href="https://proquest-safaribooksonline-com.proxy.library.ucsb.edu:9443/book/programming/python/9781491912126"> <i>Python Data Science Handbook</i></a>.

Instructions

We will work through this notebook together. To run a cell, click on the cell and press “Shift” + “Enter” or click the “Run” button in the toolbar at the top.

🐍     This symbol designates an important note about Python structure, syntax, or another quirk.

▶️     This symbol designates a cell with code to be run.

✏️     This symbol designates a partially coded cell with an example.

Introduction to NumPy

numpy

NumPy, an abbreviation for Numerical Python, is the core library for scientific computing in Python. In addition to manipulation of array-based data, NumPy provides an efficient way to store and operate on very large datasets. In fact, nearly all Python packages for data storage and computation are built on NumPy arrays.

This exercise will provide an overview of NumPy, including how arrays are created, NumPy functions to operate on arrays, and array math. While most of the basics of the NumPy package will be covered here, there are many, many more operations, functions, and modules. As always, you should consult the NumPy Docs to explore its additional functionality.

Before jumping into NumPy, we should take a brief detour through importing libraries in Python. While most packages we will use – including NumPy – are developed by third-parties, there are a number of “standard” packages that are built into the Python API. The following table contains a description of a few of the most useful modules worth making note of.

Module Description Syntax
os Provides access to operating system functionality import os
math Provides access to basic mathematical functions import math
random Implements pseudo-random number generators for various distributions import random
datetime Supplies classes for generating and manipulating dates and times import datetime as dt 
🐍 <b>Import syntax.</b> 
As we've seen already, modules and packages can be loaded into a script using an <code>import</code> statement: <code>import [module]</code> for the entire module, or <code>from [module] import [identifier]</code> to import a certain class of the module. All modules and packages used in a program should be imported at the beginning of the program.

Many packages are imported with standard abbreviations (such as dt for the datetime module) using the following syntax:

import [module] as [name]

The standard syntax for importing NumPy is:

import numpy as np 

▶️ <b> Run the cell below. </b>
Code 
import numpy as np

NumPy Arrays

The n-dimensional array object in NumPy is referred to as an ndarray, a multidimensional container of homogeneous items – i.e. all values in the array are the same type and size. These arrays can be one-dimensional (one row or column vector), two-dimensional (m rows x n columns), or three-dimensional (arrays within arrays).

Constructing arrays from lists

There are two main ways to construct NumPy arrays. The first involves using the np.array() function to generate an array from one or more lists:

np.array([8,0,9,1,4])
>>> array([8, 0, 9, 1, 4])

Recall that unlike lists, all elements within an array must be of the same type. If the types do not match, NumPy will “upcast” if possible (e.g. convert integers to floats):

np.array([8.14,0.12,9,1.77,4])
>>> array([8.14, 0.12, 9.  , 1.77, 4.  ])

In these examples, we have created one-dimensional arrays. By default, elements in a one-dimensional array are cast as rows in a column (i.e. a column vector). If, however, we wanted a row vector instead, we could use double brackets [[]] to create an array with one row and multiple columns:

np.array([[8,0,9,1,4]]) # row vector with 5 columns
>>> array([[8, 0, 9, 1, 4]])

This is because NumPy treats the inner element(s) or list(s) as rows. This is easier to see with a multidimensional array:

np.array([[3,2,0,1],[9,1,8,7],[4,0,1,6]]) # array with 3 rows x 4 columns

>>> array([[3, 2, 0, 1],
           [9, 1, 8, 7],
           [4, 0, 1, 6]])

Constructing arrays using functions

Oftentimes, it will be more efficient to construct arrays from scratch using NumPy functions. The np.arange() function is used to generate an array with evenly spaced values within a given interval. np.arange() can be used with one, two, or three parameters to specify the start, stop, and step values. If only one value is passed to the function, it will be interpreted as the stop value:

# Create an array of the first seven integers 
np.arange(7)
>>> array([0, 1, 2, 3, 4, 5, 6])

# Create an array of floats from 1 to 12
np.arange(1.,13.)
>>> array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12.])

# Create an array of values between 0 and 20, stepping by 2
np.arange(0,20,2)
>>> array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])

Similarly, the np.linspace() function is used to construct an array with evenly spaced numbers over a given interval. However, instead of the step parameter, np.linspace() takes a num parameter to specify the number of samples within the given interval:

# Create an array of 5 evenly spaced values between 0 and 1
np.linspace(0,1,5)
>>> array([0.  , 0.25, 0.5 , 0.75, 1.  ])

Note that unlike np.arange(), np.linspace() includes the stop value by default (this can be changed by passing endpoint=True). Finally, it should be noted that while we could have used np.arange() to generate the same array in the above example, it is recommended to use np.linspace() when a non-integer step (e.g. 0.25) is desired.

There are several functions that take a shape argument to generate single-value arrays with specified dimensions passed as a tuple (rows,columns):

# Create a 1D array of zeros of length 4
np.zeros(4)
>>> array([0., 0., 0., 0.]

# Create a 4 x 3 array filled with zeros
np.zeros((4,3))
>>> array([[0., 0., 0.],
           [0., 0., 0.],
           [0., 0., 0.],
           [0., 0., 0.]])

# Create a 4 x 3 array filled with ones
np.ones((4,3))
>>> array([[1., 1., 1.],
           [1., 1., 1.],
           [1., 1., 1.],
           [1., 1., 1.]])


# Create a 4 x 3 array filled with 3.14
np.full((4,3),9.87)
>>> array([[9.87, 9.87, 9.87],
           [9.87, 9.87, 9.87],
           [9.87, 9.87, 9.87],
           [9.87, 9.87, 9.87]])

The np.random.rand() function is used to generate n-dimensional arrays filled with random numbers between 0 and 1:

# Create a 4 x 3 array of uniformly distributed random values
np.random.rand(4,3)
>>> array([[0.17461878, 0.74586348, 0.9770975 ],
           [0.77861373, 0.28807114, 0.10639001],
           [0.09845499, 0.36038089, 0.58533369],
           [0.30983962, 0.74786381, 0.27765305]])

As we will see, the np.random.rand() function is very useful for sampling and modeling.

The last array-construction function we will consider (but by no means the last in the NumPy API!) is the np.eye() function, which is used to generate the two-dimensional identity matrix:

# Create a 4 x 4 identity matrix
np.eye(4)
>>> array([[1., 0., 0., 0.],
           [0., 1., 0., 0.],
           [0., 0., 1., 0.],
           [0., 0., 0., 1.]])

Lastly, it’s worth noting that nearly all of these functions contain an optional dtype parameter, which can be used to specify the data-type of the resulting array (e.g. np.ones((4,3),dtype=int) would return a 4 x 3 array of ones as integers, rather than the default floats).

Array Manipulation

Having established how to construct arrays in NumPy, let’s explore some of the attributes of the ndarray, including how to manipulate arrays. Nearly all data manipulation in Python involves NumPy array manipulation; many other Python data tools like Pandas (Session 2-2) are built on the NumPy array. Thus, while many of the examples below may seem trivial, understanding these operations will be critical to understanding more complex operations and Python data manipulation more broadly.

Array attributes

Array attributes are properties that are intrinsic to the array itself. While there are quite a few attributes of NumPy arrays, the ones we will use most often provide information about the size, shape, and type of the arrays:

Method Description
ndarray.ndim Number of array dimensions
ndarray.shape Tuple of array dimensions (rows, columns)
ndarray.size Total number of elements in the array
ndarray.dtype Data-type of array elements

For example, let’s create a random two-dimensional array and explore its attributes using the above methods.

# Initialize array
a = np.random.rand(4,7)

# Determine array dimensions
a.ndim
>>> 2

# Determine array shame
a.shape
>>> (4, 7)

# Determine array size
a.size
>>> 28

# Determine data-type
a.dtype
>>> dtype('float64')

✏️ Try it.

Construct two array vectors, a column vector and a row vector, from the list [8,0,9,1,4], as in the first example. Using the ndarray.ndim and ndarray.shape methods, show the difference between constructing an array with single vs. double brackets.

Indexing + slicing

Indexing arrays is analogous to indexing lists:

# Initialize a one-dimensional array
x1 = np.array([8,0,9,1,4])

# Return the value in position 1
x1[1]
>>> 0

With multidimensional arrays, a tuple of indices can be passed to access the rows and columns of an array: ndarray[row,column]. If a single index is passed, the corresponding row element will be returned:

# Initialize a two-dimensional array
x2 = np.array([[3,2,0,1],
               [9,1,8,7],
               [4,0,1,6]])

# Return the value of the element in the 2nd row, 3rd column
x2[1,2]
>>> 8 

# Return the entire second row
x2[1]
>>> array([9, 1, 8, 7])

Slicing of arrays allows you to access parts of arrays or subarrays. Just like with lists, slicing follows the syntax ndarray[start:stop:step].

# Return the elements in positions 1-4
x1[1:]
>>> array([0, 9, 1, 4])

For multidimensional arrays, a tuple of slices is used: ndarray[row_start:row_end:row_step, col_start:col_end:col_step].

# Return the entire third column
x2[:,2]
>>> array([0, 8, 1])

# Return the first two rows and two columns
x2[:2,:2]
>>> array([[3, 2],
           [9, 1]])

# Return all rows and every other column
x2[:,::2]
>>> array([[3, 0],
           [9, 8],
           [4, 1]])
Code 
<h4 style="border:1px; border-style:solid; border-color:black; padding: 0.5em;"> <span style="color:black"> Array reduction </span> </h4>

**Array reduction** refers to the computation of summary statistics on an array – i.e. *reducing* an array to a single aggregate value, such as the mean, minimum, maximum, etc. These array reduction methods are similar to those used for lists:

```python
x2 = np.array([[3,2,0,1],
               [9,1,8,7],
               [4,0,1,6]])

# Sum of all values in array
x2.sum()
>>> 42

# Maximum value of the array
x2.max()
>>> 9

# Minimum value of the array
x2.min()
>>> 0

# Mean value of the array
x2.mean()
>>> 3.5

# Standard deviation of the array
x2.std()
>>> 3.095695936834452

```

All of these methods can be passed with an *`axis`* argument, which allows for aggregation across the rows or columns of the array. In NumPy – as well as the many libraries built on NumPy, axis `0` always refers to the *rows* of an array, while axis `1` refers to the *columns*:

```python
# Mean of each row (calculated across columns)
x2.mean(axis=1)
>>> array([1.5 , 6.25, 2.75])

# Maximum value of each column (calculated across rows)
x2.max(axis=0)
>>> array([9, 2, 8, 7])
```
🐍 <b>Functions vs. Methods.</b> 
As we'll explore later in this course, <i>functions</i> and <i>methods</i> in Python are essentially the same thing. The key difference, however, is that functions can be called generically, while methods are always attached to and called on objects. It is also worth noting that while a method may alter the object itself, a function <i>usually</i> simply operates on an object without changing it, and then prints something or returns a value.

For each of the array reduction methods demonstrated above, there is a corresponding function. For example, the mean of an array can be calculated using the method ndarray.mean() or the function np.mean(ndarray).

These – and the many additional – aggregation functions in NumPy can be used, not only on arrays, but on any numerical object.

Reshaping, resizing, + rearranging arrays

Other useful array operations include reshaping, resizing, and rearranging arrays. The ndarray.reshape() method is used to change the shape of an array:

# Initialize a one-dimensional array with 16 elements
a = np.arange(1.0,17.0)

a
>>> array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12., 13.,
       14., 15., 16.])

# Reshape array a into a 4x4 array
b = a.reshape(4,4)

b
>>> [[ 1.  2.  3.  4.]
     [ 5.  6.  7.  8.]
     [ 9. 10. 11. 12.]
     [13. 14. 15. 16.]]

There are a few important things to note about the ndarray.reshape() method. First and unsurprisingly, the size of array must be preserved (i.e. the size of the reshaped array must match that of the original array). Secondly, and perhaps more importantly, the ndarray.reshape() method creates a view of the original array a, rather than a copy, which would allow the two variables to exist independently. Because b is a view of a, any changes made to b will also be applied to a:

# Reset the value in the third row, third column (11.0)
b[2,2] = 0.0

b
>>> array([[ 1.,  2.,  3.,  4.],
           [ 5.,  6.,  7.,  8.],
           [ 9., 10.,  0., 12.],
           [13., 14., 15., 16.]])

a
>>> array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.,  0., 12., 13., 
           14., 15., 16.])

Unlike ndarray.reshape(), the ndarray.resize() method operates in-place on the original array. The ndarray.resize() method is used to add or delete rows and/or columns:

# Initialize a 2 x 3 array
a = np.array([[1,2,3],[4,5,6]])

# Copy the original array
smaller = a.copy()
# Use ndarray.resize() to reshape to a 2x2 array and delete the last two elements
smaller.resize(2,2)

smaller
>>> array([[1, 2],
           [3, 4]])

# Copy the original array
bigger = a.copy()
# Use ndarray.resize() to reshape to a 6x6 array by adding zeros
bigger.resize(6,6)

bigger
>>> array([[1, 2, 3, 4, 5, 6],
           [0, 0, 0, 0, 0, 0],
           [0, 0, 0, 0, 0, 0],
           [0, 0, 0, 0, 0, 0],
           [0, 0, 0, 0, 0, 0],
           [0, 0, 0, 0, 0, 0]])
🐍 <b>Copies vs. Views</b> 
This is just one example of many occasions when it is advisable to create a <b>copy</b> of the original object before manipulating it. Had we not copied <code>a</code> before resizing it to a 2x2 array, the last two elements would have been permanently deleted, as <code>a</code> itself would have been resized. A good rule of thumb is to <b>always create a copy</b> before changing or deleting any data.

Often it is useful to rearrange the elements in an array. The ndarray.transpose() method – or simply ndarray.T, transposes the array, switching the rows and columns, while the np.flip(), np.flipud(), and np.fliplr() functions reverse the order of elements in the array along a given axis:

# Initialize a new 4x5 array
x = np.array([[4, 2, 0, 1, 5],
              [9, 4, 1, 3, 0],
              [6, 0, 8, 5, 9],
              [7, 3, 2, 7, 4]])

# Transpose rows + columns
x.T
>>> array([[4, 9, 6, 7],
           [2, 4, 0, 3],
           [0, 1, 8, 2],
           [1, 3, 5, 7],
           [5, 0, 9, 4]])

# Flip the array (reverse the order of all elements)
np.flip(x)
>>> array([[4, 7, 2, 3, 7],
           [9, 5, 8, 0, 6],
           [0, 3, 1, 4, 9],
           [5, 1, 0, 2, 4]])

# Flip the array up/down (reverse the order of the rows)
np.flipud(x)
>>> array([[7, 3, 2, 7, 4],
           [6, 0, 8, 5, 9],
           [9, 4, 1, 3, 0],
           [4, 2, 0, 1, 5]])

# Flip the array left/right (reverse the order of the columns)
np.fliplr(x)
>>> array([[5, 1, 0, 2, 4],
           [0, 3, 1, 4, 9],
           [9, 5, 8, 0, 6],
           [4, 7, 2, 3, 7]])

When passed with the axis argument, np.flip() mimics the np.flipud() and np.fliplr() functions:

# Flip the array over the row axis (same as np.flipud(x))
np.flip(x, axis=0)
>>> array([[7, 3, 2, 7, 4],
           [6, 0, 8, 5, 9],
           [9, 4, 1, 3, 0],
           [4, 2, 0, 1, 5]])

# Flip the array over the column axis (same as np.fliplr(x))
np.flip(x, axis=1)
>>> array([[5, 1, 0, 2, 4],
           [0, 3, 1, 4, 9],
           [9, 5, 8, 0, 6],
           [4, 7, 2, 3, 7]])

Joining + splitting arrays

So far, we have considered array manipulation routines that operatee on a single array. We will encounter many scenarios in which it is necessary to combine multiple arrays into one or, conversely, to split a single array into two or more separate objects.

Concatenation in computer programming refers to the process of joining multiple objects end-to-end. The most common way of concatenating arrays in NumPy is with the np.concatenate() function, which takes a tuple of arrays:

# Initialize a 3x3 array
x = np.array([[4,2,0],
              [9,4,1],
              [6,0,8]])
# Initialize a 1x3 array
y = np.array([[2,8,6]])

# Concatenate x and y
np.concatenate((x,y))
>>> array([[4, 2, 0],
           [9, 4, 1],
           [6, 0, 8],
           [2, 8, 6]])

Note that, by default, np.concatenate() operates along the row axis (0). To concatenate along the column axis, we must specify axis=1 as an argument:

# Concatenate x and y along the column axis
np.concatenate((x,y), axis=1)
>>> ---------------------------------------------------------------------------
    ValueError                                Traceback (most recent call last)
    <ipython-input-65-6c2205ef28d2> in <module>
          5 y = np.array([[2,8,6,0]])
          6 
    ----> 7 np.concatenate((x,y),axis=1)

    <__array_function__ internals> in concatenate(*args, **kwargs)

    ValueError: all the input array dimensions for the concatenation axis must match exactly, but along 
    dimension 0, the array at index 0 has size 3 and the array at index 1 has size 1

Uh-oh! Unsurprisingly, when we tried to concatenate an array with 1 row to an array with 3 rows, we got a ValueError. For np.concatenate() to work, the dimensions must match. Thus, we must first transpose y before adding it to x as a column:

# Transpose y and concatenate x and y along the column axis
np.concatenate((x,y.T),axis=1)
>>> array([[4, 2, 0, 2],
           [9, 4, 1, 8],
           [6, 0, 8, 6]])

Equivalently, we could use the np.vstack() or np.hstack() function to concatenate directly along the row or column axis, respectively:

# Stack rows of x and y (same as np.concatenate((x,y), axis=0)
np.vstack((x,y))
>>> array([[4, 2, 0],
           [9, 4, 1],
           [6, 0, 8],
           [2, 8, 6]])

# Stack columns of x and y (same as np.concatenate((x,y), axis=1)
np.hstack((x,y.T))
>>> array([[4, 2, 0, 2],
           [9, 4, 1, 8],
           [6, 0, 8, 6]])

Conversely, splitting allows you to breakdown a single array into multiple arrays. Splitting is implemented with the np.split(), np.vsplit(), and np.hsplit() functions.

# Initialize a 4x3 array
z = np.array([[4, 2, 0],
              [9, 4, 1],
              [6, 0, 8],
              [2, 8, 6]])

# Split z into two arrays at row 1
np.split(z,[1])
>>> [array([[4, 2, 0]]), array([[9, 4, 1],
                                [6, 0, 8],
                                [2, 8, 6]])]

# OR
np.vsplit(z,[1])
>>> [array([[4, 2, 0]]), array([[9, 4, 1],
                                [6, 0, 8],
                                [2, 8, 6]])]

# Split z into two arrays at column 1
np.hsplit(z,[1])
>>> [array([[4],
            [9],
            [6],
            [2]]), 
     array([[2, 0],
            [4, 1],
            [0, 8],
            [8, 6]])]

Multiple indices can be passed to the np.split() and related functions, with n indices (split points) resulting in n + 1 subarrays.

Array Math

One of the key advantages of NumPy is its ability to perform vectorized operations using universal functions (ufuncs), which perform element-wise operations on arrays very quickly. For example, say we had a very large list of data, and we wanted to perform some mathematical operation on all of the data elements. We could store this data as a list or an ndarray:

# Create a list of the first 10,000 integers
a = list(range(10000))

# Create a one-dimensional array of the first 10,000 integers
b = np.arange(10000)

Now, let’s multiply each element in our dataset by 2. We can accomplish this by using a for loop for the list a and a ufunc for array b. (The %timeit module is a built-in Python function used to calculate the time it takes to execute short code snippets.)

# Use a for loop to multiply every element in a by 2
%timeit [i*2 for i in a]
# Use a ufunc to multiply every element in b by 2
%timeit b * 2

>>> 388 µs ± 30.6 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
    3.58 µs ± 41.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

The %timeit module is a built-in Python function used to calculate the time it takes to execute short code snippets.

▶️ <b> Run the cell below. </b>
Code 
# Create a list of the first 10,000 integers
list10 = list(range(10000))
# Use a for loop to multiply every element in a by 2
%timeit [i*2 for i in list10]

# Create a one-dimensional array of the first 10,000 integers
array10 = np.arange(10000)
# Use a ufunc to multiply every element in b by 2
%timeit array10 * 2
361 µs ± 2.25 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
4.18 µs ± 33.5 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

As you can see, the for loop took about 100 times longer than the exact same element-wise array operation!

Computation on single arrays using ufuncs

Ufuncs are fairly straightforward to use, as they rely on Python’s native operators (e.g. +, -, *, /):

# Create a 2x4 array of floats
x  = np.array([[1.,2.,3.,4.],
               [5.,6.,7.,8.]])

# Do some math
# Addition
x + 12
>>> array([[13., 14., 15., 16.],
           [17., 18., 19., 20.]])

# Subtraction
x - 400
>>> array([[-399., -398., -397., -396.],
           [-395., -394., -393., -392.]])

# Exponentiation
x ** 2
>>> array([[ 1.,  4.,  9., 16.],
           [25., 36., 49., 64.]])

# Combine operations
10 ** (x/2)
>>> array([[3.16227766e+00, 1.00000000e+01, 3.16227766e+01, 1.00000000e+02],
           [3.16227766e+02, 1.00000000e+03, 3.16227766e+03, 1.00000000e+04]])

These arithmetic operators act as wrappers (effectively shortcuts) around specific built-in NumPy functions; for example, the + operator is a convenient shortcut for the np.add() function:

x + 2
>>> array([[ 3.,  4.,  5.,  6.],
           [ 7.,  8.,  9., 10.]])

np.add(x,2)
>>> array([[ 3.,  4.,  5.,  6.],
           [ 7.,  8.,  9., 10.]])

The following table contains a list of arithmetic operators implemented by NumPy. Note that these functions work on all numerical objects, not just arrays.

Arithmetic functions in NumPy
Operator ufunc Description
+ np.add() Addition
- np.subtract() Subtraction
* np.multiply() Multiplication
/ np.divide() Division
// np.floor_divide() Floor division (returns largest integer)
** np.power() Exponentiation
% np.mod() Modulus/remainder
**(1/2) np.sqrt() Square root-alize

Furthermore, as a numerical package, NumPy implements many additional mathematical operations for use in Python – on arrays or otherwise. The following tables show some of the more commonly used mathematical functions in NumPy. The x is used to denote a numerical object – this could be an int, float, list, ndarray, etc.

Logarithmic functions
ufunc Operation
np.exp(x) e^x
np.log(x) \ln x
np.log10(x) \log x

Trigonometric functions
ufunc Description
np.sin(x) \sin{x}
np.cos(x) \cos{x}
np.tan(x) \tan{x}
np.arcsin(x) \sin^{-1}{x}
np.arccos(x) \cos^{-1}{x}
np.arctan(x) \tan^{-1}{x}

Note: NumPy assumes all inputs to trigonometic functions are in units of radians. The np.radians() function can be used to convert from degrees to radians, while the np.degrees() function does the opposite.

Useful mathematical constants
Constants Description
np.e e
np.pi \pi

Array-to-array math

So far, we have only considered operations between a single array and an integer, but often it is necessary to perform mathematical operations on multiple arrays. Much like NumPy handles single array operations, array-to-array math in NumPy uses ufuncs to perform element-wise calculations. For arrays of the same dimensions, this is straight forward:

x  = np.array([[1.,2.,3.,4.],
               [5.,6.,7.,8.]])

y = np.array([[9.,87.,3.,5.6],
              [-1.,4.,7.1,8.]])

# Addition
x + y
>>> array([[10. , 89. ,  6. ,  9.6],
           [ 4. , 10. , 14.1, 16. ]])

# Division
x / y
>>> array([[ 0.11111111,  0.02298851,  1.        ,  0.71428571],
           [-5.        ,  1.5       ,  0.98591549,  1.        ]])

For arrays whose dimensions do not match, NumPy does something called broadcasting. So long as one dimension of each array matches and one array has a dimension of 1 in one direction, the smaller array is “broadcast” to the dimensions of the larger array. In this process, the row or column is replicated to match the dimensions of the larger array. This is best illustrated in the following diagram:

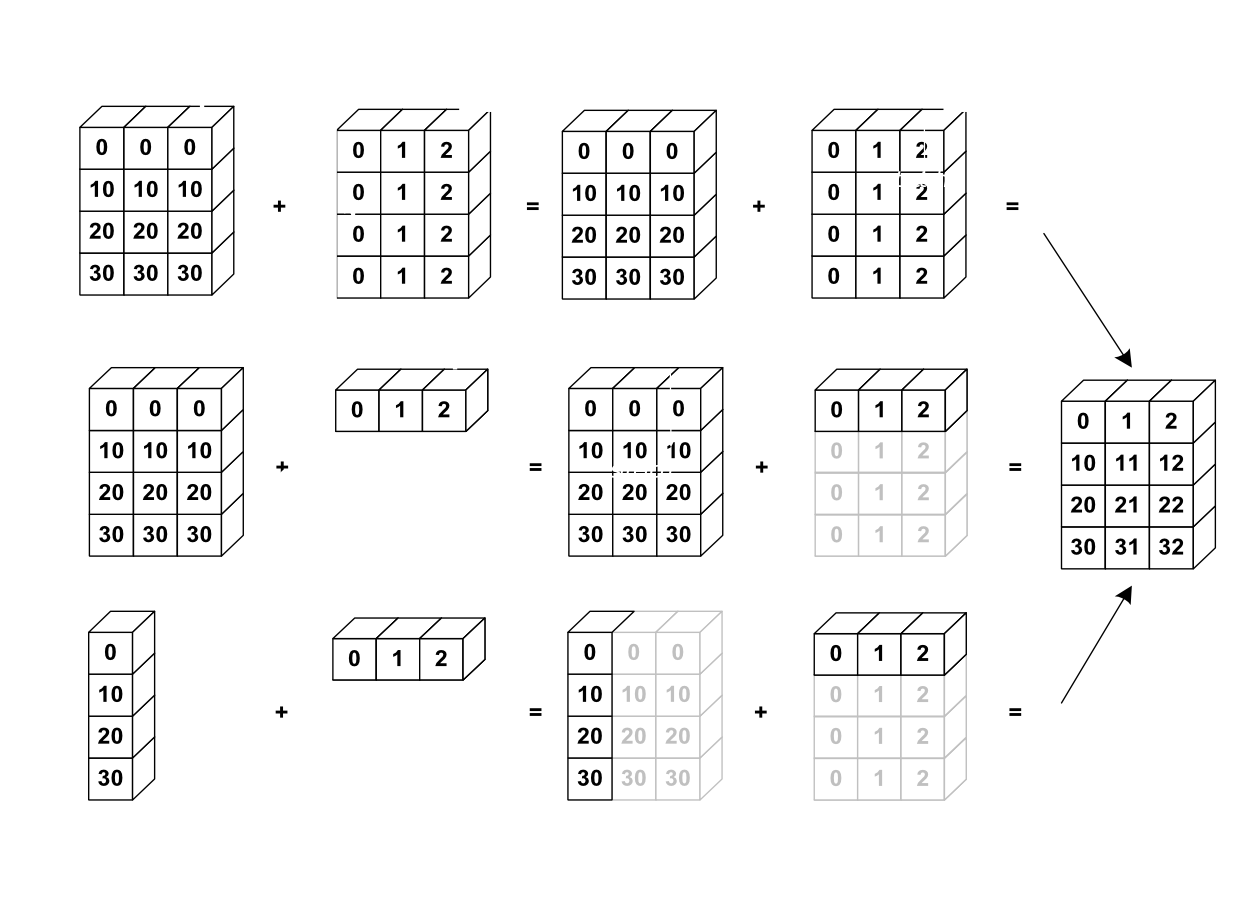
broadcasting

a = np.array([[1.,2.,3.,4.],
             [5.,6.,7.,8.]])

b = np.array([10,11,12,13])

c = np.array([[1.],
             [20.]])

# Row-wise
a + b
>>> array([[11., 13., 15., 17.],
           [15., 17., 19., 21.]])

# Column-wise
a + c
>>> array([[ 2.,  3.,  4.,  5.],
           [25., 26., 27., 28.]])

# Multiple operations
a + c**2
>>> array([[  2.,   3.,   4.,   5.],
           [405., 406., 407., 408.]])

Missing Data

Most real-world datasets – environmental or otherwise – have data gaps. Data can be missing for any number of reasons, including observations not being recorded or data corruption. While a cell corresponding to a data gap may just be left blank in a spreadsheet, when imported into Python, there must be some way to handle “blank” or missing values.

Missing data should not be replaced with zeros, as 0 can be a valid value for many datasets, (e.g. temperature, precipitation, etc.). Instead, the convention is to fill all missing data with the constant NaN. NaN stands for “Not a Number” and is implemented in NumPy as np.nan.

NaNs are handled differently by different packages. In NumPy, all computations involving NaN values will return nan:

data = np.array([[2.,2.7.,1.89.],
                 [1.1, 0.0, np.nan],
                 [3.2, 0.74, 2.1]])

data.mean()
>>> nan

In this case, we’d want to use the alternative np.nanmean() function, which ignores NaNs:

data.nanmean()
>>> 1.71625

NumPy has several other functions – including np.nanmin(), np.nanmax(), np.nansum() – that are analogous to the regular ufuncs covered above, but allow for computation of arrays containing NaN values.

Wrapping up

The topics covered in this session are but a small window into the wide world of NumPy, but by now you should be familiar with the basic objects and operations in the NumPy library, which are the building blocks of data science in Python. As always – especially now that we’ve begun exploring third-party packages – refer to the NumPy docs for comprehensive information on all functions, methods, routines, etc. and to check out more of NumPy’s capabilities.

Next, we’ll explore one of data scientists’ favorite libraries: 🐼.